Answer:
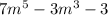
Explanation:
Given expression
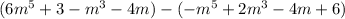
Write subtraction of a polynomial expression as addition of the additive inverse .Therefore we can write expression as
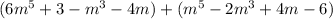
Rewrite terms that are subtracted as addition of the oppostite .Therefore , we can write expression as
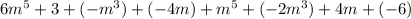
Grouping og like terms . Then we get the expession is given by
![[6m^5+m^5]+[3+(-6)]+[(-m^3)+(-2m^3)]+[(-4m)+4m]](https://img.qammunity.org/2019/formulas/mathematics/college/iil6rkdzy93nvieckh90m24g24ts38qenc.png)
Combine like terms then we can write expression

Write the resulting polynomial in standard form
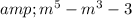 .
.
(6m^5+3-m^3-4m)-(-m^5+2m^3-4m+6)=m^5-m^3-3.