From the description, we have the function
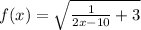
Since the square root cannot be a negative number, the only thing need to do to find the domain of the function

is take the expression inside the square rot and set it greater or equal than zero:
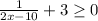
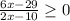
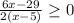

or
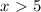
We can conclude that we can use the inequality
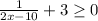
to find the domain of

. Also, the domain of

is (∞,
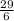
]U(5,∞).