Question

What is the pressure of 0.5 mol nitrogen (N2) gas in a 5.0 L container at 203 K?

Answer 1

you need to use the universal gas equation. in order to find pressure you will have to transpose it to be P= nRT/V
substitute the values in: P = 0.5×8.31×203/5.0
which will give you 168.693 and when rounded to the correct significant figure it would be 169kPa.

Answer 2

The pressure of the nitrogen in the container is 168.774 kPa

Step-by-step explanation:

The volume, pressure, temperature and mol of a gas are linked through the ideal gas law which is:

p . V = n . R . T

Where p is the pressure of the gas, V the volume of the gas, n the amount of moles of the gas, T the temperature of the gas and R the universal gas constant.

The universal gas constant R we will be using is:

`R= 8.314(L . kPa)/(K . mol)`

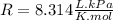
For example, What is the temperature of 4 mol of gas in a 10 Liters container at 300kPa?

The data is:

V = 10L

p = 300kPa

n = 4 moles

`R= 8.314(L . kPa)/(K . mol)`

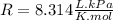
T = ?

Now we put the data in the equation and calculate the temperature.

10L ⋅ 300kPa = 4mol ⋅
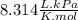`8.314(L . kPa)/(K . mol)` ⋅ T

T = 10L· 300kPa÷4mol ⋅
`8.314(L . kPa)/(K . mol)`

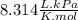
T= 90.21 K

So, knowing all the data except one, using the ideal gas law we can calculate it.

The equation for this case would be:

p = 0.5mol ·
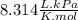`8.314(L . kPa)/(K . mol)` · 203K ÷ 5.0L

And the result:

p = 168.774 kPa