Question

23)   Does the following infinite geometric series diverge or converge? Explain.

1/7+1/28+1/112+1/448+....


It diverges; it has a sum.


It converges; it does not have a sum.


It diverges; it does not have a sum.


It converges; it has a sum.

Answer 1

it diverges; it does not have a sum.  the sum of a geometric series is given by a /(1-r) where a is the first term and the r is the ratio between the terms. r=3 in the series you have given . The absolute value of r must be less then 1 for a geometric series to converge.

Answer 2

Answer: The correct option is (D) It converges; it has a sum.

Step-by-step explanation: We are given to check whether the following infinite geometric series diverge or converge :

`(1)/(7)+(1)/(28)+(1)/(112)+(1)/(448)+~~.~~.~~.`

We know that

an infinite geometric series converges if the modulus of the common ratio is less than 1.

For the given geometric series, the common ratio r is given by

`r=((1)/(28))/((1)/(4))=((1)/(112))/((1)/(28))=((1)/(448))/((1)/(112))=~~.~~.~~.~~=(1)/(4).`

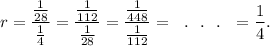
So, we get

`|r|=|(1)/(4)|=0.25<1.`

Therefore, the given infinite geometric series converges.

Also, we know that the sum of a convergent infinite geometric series with first term a and common ratio r is given by

`S=(a)/(1-r).`

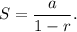
For the given series,

`a=(1)/(7),~~r=(1)/(4).`

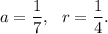
Therefore, the required sum will be

`S=(a)/(1-r)=((1)/(7))/(1-(1)/(4))=((1)/(7))/((3)/(4))=(1)/(7)*(4)/(3)=(4)/(21).`

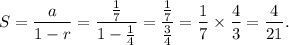
Thus, the given series is convergent and it has a sum of
`(4)/(21).`

Option (D) is CORRECT.