Question

Which statement describes the domain of the function f(x) = 3x / 4x2-4 ?

A. all real numbers
B. all nonzero real numbers
C. all real numbers except x = 3/4
D. all real numbers except x = –1 and x = 1

Answer 1

Answer: D. All real numbers except x = –1 and x = 1

Explanation:

Given function,

`f(x) = (3x)/(4x^2-4)`

which is the rational function,

Since, a rational function is defined for all real numbers except for those numbers for which the denominator of the rational function is equal to zero.

Here, the denominator of the given rational function =
`4x^2 - 4`

`\text{ When }4x^2 - 4 = 0`

⇒
`(2x+2)(2x-2) = 0`

⇒
`\text{ if } 2x+2 = 0\implies x = -1`

Or
`\text{ if } 2x-2 = 0\implies x = 1`

Thus, the function can not defined when x = -1 or x = 1,

⇒ The given rational function is defined for all real numbers except x = -1, and x = 1.

⇒ Option D is correct.

Answer 2

Given rational function:
`f(x)=(3x)/(4x^2-4)`.

We need to find the domain of the given rational function.

In order to find the domain, we need to find the restrictions of the domain.

In order to find the restrictions, we need to set denominator equal to 0 and solve for x.

Therefore,

`4x^2-4 =0`

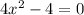
Adding 4 on both sides, we get

`4x^2+4 -4 = 0+4`

`4x^2 = 4.`

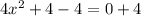
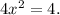
Dividing both sides by 4, we get

`(4x^2)/(4) = (4)/(4)`

`x^2=1`

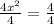
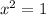
Taking square root on both sides, we get

`√(x^2) =√(1)`

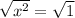
x = +1, =-1.

Therefore, domain is all real numbers except x = –1 and x = 1.

So, the correct option is D. all real numbers except x = –1 and x = 1.