Question

How do you find the asymptote of a function

Answer 1

There are two types of aymptotes; horizontal and vertical asymptote. To find asymptotes of a function, you first must know the domain and range of the given function. Let's say the function is:

`f(x) = (x + 2)/(x - 2)`
Horizontal Asymptote:
To find this asymptote, we have to look at the domain (or the denominator). The domain will be: x such that x is not = to 2. This is because the denominator is x-2, and if you substitute x with 2 it will be 2-2=0. But, anything divided by 0 is undefined. To find the asymptote,you take the denominator itself;

`x - 2`

`x = 2 \: will \: be \: the \: horizontal \: asymptote`
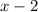
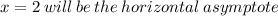
Vertical Asymptote:
To find this asymptote, we have to look at the range of the function by finding the inverse of the given function. From the given function;

`f(x) = (x + 2)/(x - 2)`
We now write y instead of f(x).

`y = (x + 2)/(x - 2)`
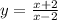
Now, interchange the variables.

`x = (y + 2)/(y - 2)`
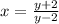
Now,make y the subject in order to get the inverse of the function.

`x(y - 2) = y + 2`

`xy - 2x = y + 2`

`xy - y = 2x + 2`

`y(x - 1) = 2x + 2`

`y = (2x + 2)/(x - 1)`
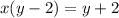
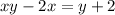
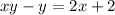
The range will be x is not equal to 1, since the result will be 0, and,
Therefore, the asymptote will be obtained by looking at the denominator of the inverse of the function; i.e.

`x - 1`

`x = 1`
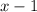
Now, replace x with letter y.

`y = 1 \: is \: the \: vertical \: asymptote`
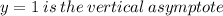
Therefore, the asymptotes have been obtained.
I hope you understand the concept.
Thank you;
kaloliavivek