Question

A farmer has 100 m of fencing to enclose a rectangular pen. Which quadratic equation gives the area (A) of the pen, given its width (w)?

Answer 1

`A(w)=50w-w^2`

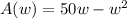
Explanation:

Let w be the width of rectangular pen.

We have been given that a framer has 100 m of fencing to enclose a rectangular pen. This means that perimeter of pen is 100 meter.

Since the perimeter is 2 times the length and width of rectangle.

`\text{Perimeter of rectangle}=2\text{ (Width+Length})`

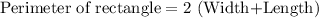
Upon substituting our given values in above formula we will get,

`100=2(w\text{+Length})`

`(100)/(2)=\frac{2(w\text{+Length})}{2}`

`50=w\text{+Length}`

`50-w=w-w\text{+Length}`

`50-w=\text{Length}`

`\text{Area of rectangle}=\text{Width*Length}`

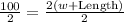
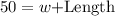
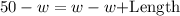
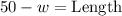
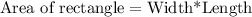
Upon substituting our given values in area formula we will get,

`\text{Area of rectangle}=w(50-w)`

`\text{Area of rectangle}=50w-w^2`

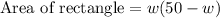
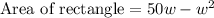
Let us represent area in terms of width of rectangle as:

`A(w)=50w-w^2`

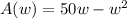
Therefore, the area of our given pen will be
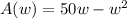`A(w)=50w-w^2`.