Question

Enny studied the characteristics of two species of bacteria. The number of bacteria of species A, A(t), after t hours is represented by the function, A(t) = 5 + (0.25t)3. The number of bacteria of species B, B(t), after t hours is represented by the function, B(t) = 2 + 8(1.06)t.

Which function describes the difference in the number of bacteria, N(t), of both the species after t hours?
N(t) = 3 + (0.25t)3 + 8(1.06)t
N(t) = 7 + (0.25t)3 + 8(1.06)t
N(t) = 7 + (0.25t)3 - 8(1.06)t
N(t) = 3 + (0.25t)3 - 8(1.06)t

Answer 1

D simply put

Explanation:

Answer 2

The number of bacteria in species A at time t is given by:
`A(t)=5+(.25t) ^(3)`.

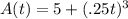
The number of bacteria in species B at time t is given by
`B(t)=2+8(1.06)t`

You are asked to find N(t) which is the difference in the species at time t. Difference refers to the answer is a subtraction problem. Thus, we are asked to find N(t) = A(t)-B(t)

We subtract and obtain:
`N(t)=5+(.25t) ^(3)-(2+8(1.06)t )=5-2+(.25t) ^(3)-(8(1.06)t )`
That is,
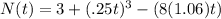
`N(t)=3+(.25t) ^(3)-(8(1.06)t )` which is the last answer choice.

With respect to notation, it is common to denote an exponent using ^. So if we want to write
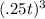
`(.25t) ^(3)` we can write "(.25t)^3"