Question

a car was bought for 45000 in 2005. if the car loses 4.5% of its value semiannually  how much will it be worth at the end of 2017? in what year will the car be worth 0

Answer 1

To solve this we are going to use the compounded interest formula:
`A=P(1+ (r)/(n) )^(nt)`
where

`A` is the final value of the car after
`t` years

`P` is the price of the car

`r` is the rate in decimal form

`n` is the number of times the rate is compounded per year

`t` is the time in years

Part 1. Notice that since the car is losing 4.5% of its value semiannually, it is losing 9% annually; also the rate is going to be negative, so
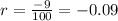
`r= (-9)/(100) =-0.09`. Since the car its value semiannually,
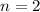
`n=2`. Also, to find
`t`, we are going to subtract 2005 from 2017:
`t=2017-2005=12`. Finally, we know for our problem that
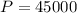
`P=45000`. Now that we have all the vales we need, lest replace them in our formula:

`A=P(1+ (r)/(n) )^(nt)`

`A=45000(1+ (-0.09)/(2) )^{(2)(12)`

`A=45000(0.955)^(24)`

`A=14903.68`

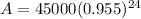
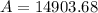
We can conclude that at the end of 2017 the char will be worth $14,903.68

Part 2. Since we want to know the year in which the price of the car will be zero,
`A=0`. From our previous calculations we know that
`P=45000`,
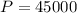
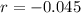
`r=-0.045`,and
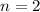
`n=2`. Lets replace those values in our formula one more time:

`A=P(1+ (r)/(n) )^(nt)`

`0=45000(1+ (-0.045)/(2) )^(2t)`
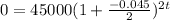
Since
`t` is the exponent, we are going to use logarithms to bring it down:

`(45000)/(0) =(1+ (-0.045)/(2) )^(2t)`

`(1+ (-0.045)/(2) )^(2t)=0`

`0.9775^(2t)=0`

`ln(0.9775^(2t))=ln(0)`

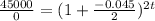
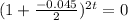
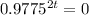
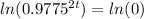
Since
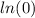
`ln(0)` cannot be evaluated (you can't divide by zero in mathematics), we can conclude that the value of the car will never be zero.