Question

Evaluate Dx / ^ 9-8x - x2^

A. Ln (-8 - 2x) + C
B. Sin -1 (x+4/5) + c
C. Sin -1 (x-4/5) + c
D. Ln ^ 9-8x-x2^ + c

My apologies if I wrote it out a little wrong and you can’t understand! Hopefully I did it right

Answer 1

It depends on what you mean by the delimiting carats "^"...

Since you use parentheses appropriately in the answer choices, I'm going to go out on a limb here and assume something like "^x^" stands for
`\sqrt x`.

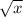
In that case, you want to find the antiderivative,


`\displaystyle\int(\mathrm dx)/(√(9-8x-x^2))`

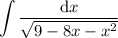
Complete the square in the denominator:


`9-8x-x^2=25-(16+8x+x^2)=5^2-(x+4)^2`

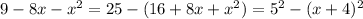
Now substitute
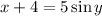
`x+4=5\sin y`, so that
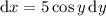
`\mathrm dx=5\cos y\,\mathrm dy`. Then


`\displaystyle\int(\mathrm dx)/(√(9-8x-x^2))=\int(5\cos y)/(√(5^2-(5\sin y)^2))\,\mathrm dy`

which simplifies to


`\displaystyle\int(5\cos y)/(5√(1-\sin^2y))\,\mathrm dy=\int(\cos y)/(√(\cos^2y))\,\mathrm dy`

Now, recall that
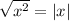
`√(x^2)=|x|`. But we want the substitution we made to be reversible, so that


`x+4=5\sin y\iff y=\sin^(-1)\left(\frac{x+4}5\right)`

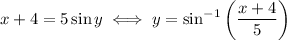
which implies that
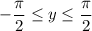
`-\frac\pi2\le y\le\frac\pi2`. (This is the range of the inverse sine function.)

Under these conditions, we have
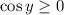
`\cos y\ge0`, which lets us reduce
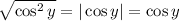
`√(\cos^2y)=|\cos y|=\cos y`. Finally,


`\displaystyle\int(\cos y)/(\cos y)\,\mathrm dy=\int\mathrm dy=y+C`

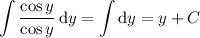
and back-substituting to get this in terms of
`x` yields


`\displaystyle\int(\mathrm dx)/(√(9-8x-x^2))=\sin^(-1)\left(\frac{x+4}5\right)+C`