Question

Find the nth term of the sequence:
14, 37, 72, 119, 178

Answer 1

Check the forward differences: if
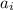
`a_i` is the
`i`-th term, then the first forward difference of
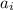
`a_i` is
`b_i=a_(i+1)-a_i`.


`\begin{cases}a_1=14\\a_2=37\\a_3=72\\a_4=119\\a_5=178\end{cases}`


`\implies\begin{cases}b_1=27-14=23\\b_2=72-37=35\\b_3=119-72=47\\b_4=178-119=59\end{cases}`

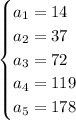
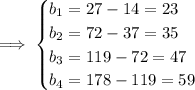
The usefulness is this: if the sequence were arithmetic, then the forward differences would be constant. For example, if the sequence were
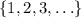
`\{1,2,3,\ldots\}`, we would see the differences to be
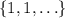
`\{1,1,\ldots\}`, and so the sequence would be growing linearly, or by an added constant.

In our case, we can compute the forward differences again (the second-order differences) until we find such a pattern. This time, we denote it by
`c_i=b_(i+1)-b_i`.


`\implies\begin{cases}c_1=35-23=12\\c_2=47-35=12\\c_3=59-47=12\end{cases}`

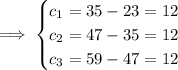
So now we know that the sequence
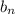
`b_n` is arithmetic with a common difference of 12 between its terms.


`b_4=b_3+12=b_2+24=b_1+36`

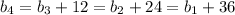
Now consider
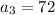
`a_3=72`; we can write this term of the sequence in terms of the previous ones. We have


`35-23=12\implies 35=23+12`

`\implies72-37=23+12`

`\implies\underbrace{72}_(a_3)=\underbrace{37}_(a_2)+\underbrace{23}_(a_2-a_1=37-14)+12`

`\implies a_3=2a_2-a_1+12`

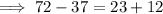
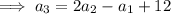
We would see a similar recursive pattern if we looked at the other terms
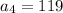
`a_4=119` and
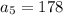
`a_5=178`. We then establish that the sequence is given by the recursive formula


`\begin{cases}a_1=23\\a_2=35\\a_(n+2)=2a_(n+1)-a_n+12&\text{for }n>2\end{cases}`

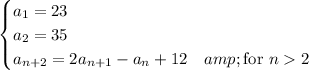
There are lots of ways to find the explicit formula for
`a_n` from this point, but the simplest is to realize that the sequence must be quadratic (this is because the second-order differences are constant) so we can assume that


`a_n=an^2+bn+c`

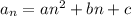
for some constants
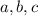
`a,b,c`. We have to solve for three unknowns, so we need three known values:


`n=1\implies14=a+b+c`

`n=2\implies37=4a+2b+c`

`n=3\implies72=9a+3b+c`


`\implies a=6,b=5,c=3`

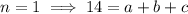
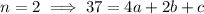
So the
`n`-th term is determined by


`a_n=6n^2+5n+3`

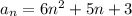
for all
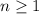
`n\ge1`.