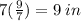Question

The perimeter of the triangle is 41 inches. The perimeter of the rectangle is 66 inches.

(Note: Pictures are not drawn to scale)
Part A: Write a system of equations to determine x and y.

Part B: Solve the system of equations. Use your solution to determine the length and width of the rectangle.

Answer 1

PART A

Perimeter is the distance around the figure.

The perimeter of the triangle is 41 inches.

This implies that,


`3x + x + 7y = 41`


`4x + 7y = 41...(1)`

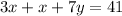
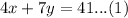
The perimeter of the rectangle is 66 inches.

This implies that,


`2(7y + 3x) = 66`
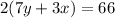
Or


`7y + 3x = 33...(2)`

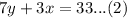
PART B

The system of equations are


`4x + 7y = 41...(1)`


`7y + 3x = 33...(2)`

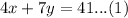
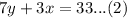
Subtract equation (2) from equation (1).

This gives us,


`4x - 3x = 41 - 33`


`x = 8`

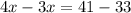
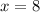
Put this value into equation (2) to find y.


`7y + 3(8) =33`


`7y + 24 = 33`


`7y = 33- 24`


`7y =9`


`y = (9)/(7)`

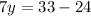
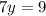
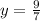
The length of the rectangle is


`3(8)=24\:in`

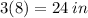
The width of the rectangle is


`7((9)/(7))=9\: in`

Answer 2

Part A) The system of equations is equal to

`41=4x+7y`

`33=(3x+7y)`

Part B)

The length is
`24\ in`

The width is
`9\ in`

Explanation:

Part A)

we know that

The perimeter of the triangle is equal to the sum of the length of its three sides

In this problem

`41=x+3x+7y`

`41=4x+7y` -----> equation A

The perimeter of rectangle is equal to

`P=2(L+W)`

In this problem

`66=2(3x+7y)`

`33=(3x+7y)` ------> equation B

Part B)

Using a graphing tool

Solve the system of equations

We know that

The intersection point both graphs is the solution of the system of equations

`41=4x+7y`

`33=(3x+7y)`

The intersection point is
`(8,9/7)`

see the attached figure

`x=8\ in`

`y=(9/7)\ in`

step 3

Find the length and width of the rectangle

The length is 3x

`3*8=24\ in`

The width is 7y

`7*(9/7)=9\ in`