Question

48 POINTS HELP ME WITH ONE GEOMETRY QUESTION I'M FAILING!!!!!!!!

HI, PLEASE HELP A BROTHA OUT I HAVE A 36 AT THE MOMENT AND I AM VERY CLOSE TO GRADUATING. HOWEVER, I'M ONLY FAILING GEOMETRY. GRADUATION IS IN 48 DAYS HELP ME

EXPLAIN IT IF YOU COULD, BUT IF YOU CAN'T THAT'S ALRIGHT

Answer 1

Looks like the line through
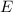
`E` and
`D` is tangent to the circle. It also looks like the
`70^\circ` is supposed to represent the measure of the arc
`CD`.

So we know the measure of the central angle subtended by the arc is also
`70^\circ`. What this means is, if you were to draw a line from
`D` to the circle's center (call it
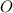
`O`), and another from the center to
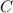
`C`, these two lines would form an angle of
`70^\circ` in the "direction" of the minor arc
`CD`.

Now
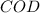
`COD` forms an isosceles triangle. We know that because the line segments
`DO` and
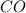
`CO` both have lengths equal to the circle's radius. Because
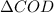
`\Delta COD` is isosceles, the angles in the triangle that don't coincide with the central angle we already know about must have the same measures. We call them both
`x^\circ`.

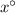
The interior angles of a triangle always add up to
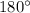
`180^\circ`, so we can easily find
`x`:


`180=x+x+70\implies x=55`

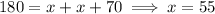
Finally, the line segments
`DO` and
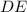
`DE` are perpendicular; this is true because
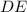
`DE` is tangent to the circle. This means the angles
`x` and the one indicated by "?" are complementary and add to
`90^\circ`.

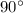
So,
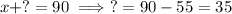
`x+?=90\implies ?=90-55=35`.