Answer:
The area of circle of spilled milk as a function of time, or A[m(t)] is
![A[m(t)]=81t^2\pi](https://img.qammunity.org/2019/formulas/mathematics/high-school/t2uopglp3b0agc5sm5ixg9h98vejeoyx85.png) . The area of spilled milk after 2 minutes is 1017.36 square unit.
. The area of spilled milk after 2 minutes is 1017.36 square unit.
Explanation:
Consider the provided information.
The milk flow can be expressed with the function m(t) = 9t, where t represents time in minutes and m represents how far the milk is spreading.
The area of the pattern can be expressed as A(m) = πm².
Part A:
To find the area of the circle of spilled milk as a function of time, substitute the value of function in area as shown:
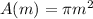
![A[m(t)]=\pi (9t)^2](https://img.qammunity.org/2019/formulas/mathematics/high-school/c2fckysejs8g6qegbnxbs5to0v9btzczh7.png)
![A[m(t)]=81t^2\pi](https://img.qammunity.org/2019/formulas/mathematics/high-school/t2uopglp3b0agc5sm5ixg9h98vejeoyx85.png)
Hence. the area of circle of spilled milk as a function of time, or A[m(t)] is
![A[m(t)]=81t^2\pi](https://img.qammunity.org/2019/formulas/mathematics/high-school/t2uopglp3b0agc5sm5ixg9h98vejeoyx85.png) .
.
Part B:
Substitute t = 2 in the above equation.
![A[m(t)]=81(2)^2\pi](https://img.qammunity.org/2019/formulas/mathematics/high-school/qik3ue4pzx2mrax1ry1hc1sm4z2fa9ayhu.png)
![A[m(t)]=81* 4* 3.14](https://img.qammunity.org/2019/formulas/mathematics/high-school/cl3ehtgpmn8g9991tjsyizc339t8ysfom0.png)
![A[m(t)]=1017.36](https://img.qammunity.org/2019/formulas/mathematics/high-school/r87o19x10aguf4guln7gq002jqqaocrl50.png)
Hence, the area of spilled milk after 2 minutes is 1017.36 square unit.