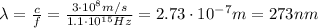Question

If the energy of 1.00 mole of photons is 441 kj, what is the wavelength of the light?

Answer 1

1 mol of photons contained a number of photons equal to Avogadro number:

`N=N_A = 6.022 \cdot 10^(23)`
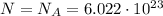
The total energy of the mole of photons is
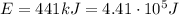
`E=441 kJ=4.41 \cdot 10^5 J`, so the energy of a single photon is the total energy divided by the number of photons:

`E_1 = (E)/(N) = (4.41 \cdot 10^5 J)/(6.022 \cdot 10^(23)) =7.32 \cdot 10^(-19)J`

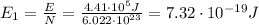
The energy of a single photon is related to its frequency f:

`E_1 = hf`
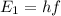
where h is the Planck constant. From this formula, we find the frequency of the photons in the problem:

`f= (E_1)/(h)= (7.32 \cdot 10^(-9) J)/(6.6 \cdot 10^(-34)Js) =1.1 \cdot 10^(15) Hz`

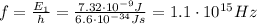
And from the frequency we can finally calculate the wavelength
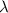
`\lambda`, using the relationship between wavelength, frequency and speed of light (c) for photons:

`\lambda= (c)/(f)= (3 \cdot 10^8 m/s)/(1.1 \cdot 10^(15) Hz) =2.73 \cdot 10^(-7) m = 273 nm`