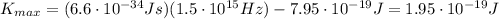Question

Light of 1.5 ✕ 1015 hz illuminates a piece of tin, which has a work function of 4.97 ev. (a) what is the maximum kinetic energy of the photoelectrons?

Answer 1

In the photoelectric effect, the energy of the incoming photon (E=hf) is used in part to extract the photoelectron from the metal (work function) and the rest is converted into kinetic energy of the photoelectron:

`hf = \phi + K`
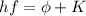
where
h is the Planck constant
f is the frequency of the incident light

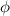
`\phi` is the work function of the material
K is the kinetic energy of the photoelectron.

The photoelectron generally loses part of its kinetic energy inside the material; however, we are interested in its maximum kinetic energy, that is the one the electron has when it doesn't lose energy, so we can rewrite the previous equation as

`K_(max) = hf - \phi`

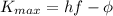
The work function is (in Joule)

`\phi = (4.97 eV)(1.6 \cdot 10^(-19) J/eV)=7.95 \cdot 10^(-19) J`

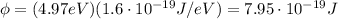
and using the data of the problem, we find the maximum kinetic energy of the photoelectrons

`K_(max) = (6.6 \cdot 10^(-34) Js)(1.5 \cdot 10^(15) Hz)-7.95 \cdot 10^(-19)J= 1.95 \cdot 10^(-19) J`