Question

Assuming a nearly frictionless ride, what can you say about a roller coaster’s potential and kinetic energy from the top to the bottom of a hill?

Answer 1

At the top of the hill, the roller coaster car only contains potential energy as it is perfectly still, so its total mechanical energy at the top of the hill would be in the form of only potential energy.

At the bottom of the hill, this potential energy would have converted all into kinetic energy, because there is no energy losses due to frictionless ride.

Step-by-step explanation:

Answer 2

The mechanical energy of the roller coaster is sum of kinetic energy K and gravitational potential energy U:

`E=K+U`
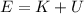
where

`K= (1)/(2)mv^2` is the kinetic energy

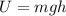
`U=mgh` is the gravitational potential energy

Since the ride is frictionless, the total mechanical energy E is conserved during the ride. Therefore, at the top of the hill, the potential energy is maximum, because h (the height) is maximum, and this means the kinetic energy is minimum (because the sum of K and U is constant), so the velocity will be minimum. Viceversa, at the bottom of the hill, the potential energy will be minimum (because h is minimum), so the kinetic energy K will be maximum, and the velocity v of the roller coaster will be maximum.