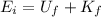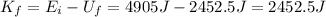Question

"a 10 kg rock is pushed off the edge of a bridge 50 meters above the ground. what was the kinetic energy of the rock at the midway point of its fall?"

Answer 1

Let's call h the initial height of the rock (h=50 m, the height of the bridge).

Initially, the rock has only gravitational potential energy, which is given by

`U_i=mgh`
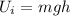
where m=10 kg is the mass of the rock while g is the gravitational acceleration. So, the total mechanical energy of the rock at this point is

`E_i = U_i = mgh=(10 kg)(9.81 m/s^2)(50 m)=4905 J`

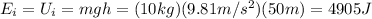
At midway point of its fall, its height is
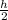
`(h)/(2)`, so its potential energy is

`U_f = mg (h)/(2) = (10 kg)(9.81 m/s^2)(25 m)=2452.5 J`
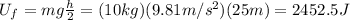
But now the rock is also moving by speed v, so it also has kinetic energy:

`K_f = (1)/(2)mv^2`
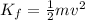
So the total energy at the midway point of the fall is

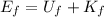
`E_f = U_f + K_f` (1)

The mechanical energy must be conserved, so
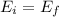
`E_i = E_f`, so we can rewrite (1) and solve it to find the kinetic energy of the rock at midway point of its fall:

`E_i = U_f + K_f`

`K_f = E_i - U_f = 4905 J - 2452.5 J=2452.5 J`