Question

Suppose now the same client as in the previous problem prefers to invest in your portfolio a proportion (y) that maximizes the expected return on the overall portfolio subject to the constraint that the overall portfolio's standard deviation will not exceed 20%. What is the maximum investment proportion, y, for the risky portfolio

Answer 1

P = 74.07%

Step-by-step explanation:

Note: An important data is missing in this question to solve for the maximum investment proportion y for the risky portfolio. I have found the similar question on the internet and I am including that missing data to complete this question in order to solve for the sack of understanding and concept.

Required: Maximum investment proportion y for the risky portfolio.

Let's denote this requirement as P for proportion.

Given Data:

Standard Deviation of investor's portfolio = 20% = 0.20

According to the formula to calculate the proportion of investment that investor wants to do in the risky portfolio, we need to have standard deviation of the risky portfolio, which is missing in this question. I have found it on the internet

Standard Deviation of the risky portfolio = 27% = 0.27

So, the formula is:

Standard deviation of the investors portfolio = Investment Portfolio x Standard deviation of the risky portfolio.

Let's suppose,

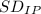`SD_(IP)` = Standard deviation of the investors portfolio

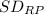`SD_(RP)` = Standard deviation of the risky portfolio.

P = Investment Proportion

So,

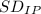`SD_(IP)` = P x
`SD_(RP)`

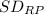
Solving for P

P =
`SD_(IP)`/
`SD_(RP)`

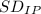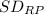
Plugging in the values.

P = 0.20/0.27

P = 0.7407 x 100

P = 74.07%

Hence, we can conclude that, investor can invest 74.07% of his investment in the risky portfolio for not exceeding the standard deviation 20% of the investor portfolio.