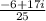Question

Write in standard complex form 2+3i \3-4i

Answer 1

The trick here is to rationalize the denominator. We don't want either an imaginary or a complex number there.

2+3i 3+4i 6+8i+9i - 12 -6 + 17i
------- * ------- = ------------------ = ------------- (answer)
3-4i 3+4i 9+16 25

Answer 2

`(-6+17i)/(25)`

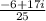
Explanation:

We are given the complex number. Here we have to rationalize the denominator. To do we have to multiply both the numerator and the denominator by conjugate of the denominator.

The conjugate of a + ib is a - ib.

We are given
`(2 + 3i)/(3 - 4i)`

The conjugate of 3 - 4i is 3 + 4i

We need to multiply both the numerator and the denominator by 3 + 4i

`(2 + 3i)/(3 - 4i) . (3 + 4i)/(3 + 4i)`

=
`(6 + 8i + 9i +12i^2)/(9 - 16i^2)`

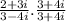
The value
`i^2 = -1`

=
`(6 + 17i +12(-1))/(9 - 16(-1))`

=
`(6 +17i -12)/(9 +16) = (-6+17i)/(25)`

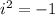
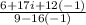
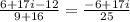
The standard complex form of the given expression is
`(-6+17i)/(25)`