Answer:
115 cars.
Explanation:
We have been given an equation
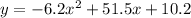 which approximates the average number of cars that pass through an intersection x hours after 3:00 p.m.
which approximates the average number of cars that pass through an intersection x hours after 3:00 p.m.
Since we know that there will be 3.5 hours between 3:00 pm and 6:30 pm. So to find the average number of cars that pass through the intersection at 6:30 pm we will substitute
 in our given equation.
in our given equation.
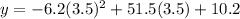
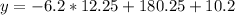
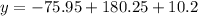
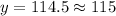
Therefore, approximately 115 cars will passe through the intersection at 6:30 pm.