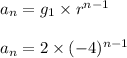Question

Find an equation for the nth term of a geometric sequence where the second and fifth terms are -8 and 512, respectively.

A) an = 2 • (-4)n + 1
B) an = 2 • 4n - 1
C) an = 2 • (-4)n - 1
D) an = 2 • 4n

Answer 1

The correct answer is C)
`a_n=2*(-4)^(n-1)`.

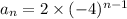
Since it is a geometric sequence, we multiply by a constant, r, each time to find the next term.

g₂ = -8
g₅ = 512

g₂ * r * r * r = g₅
-8(r)(r)(r) = 512
-8r³ = 512

Divide both sides by -8:
-8r³/-8 = 512/-8
r³ = -64

Take the cubed root of both sides:
∛r³ = ∛-64
r = -4

Now we work backward from g₂ to find g₁:

-8/-4 = 2

We have that g₁ = 2 and r = -4. This gives us


`a_n=g_1 * r^(n-1) \\ \\a_n=2 * (-4)^(n-1)`