Question

Let a be a rational number and b be an irrational number which of the following are true statements

A. The sum of A and B is never rational.
B. The product of a and b is rational
C. b^2 is sometimes rational
D. a^2 is always rational
E.√a is never rational
F.√B is never rational

Answer 1

The sum of a and b is never rational
A^2 is always rational
The square root of a is never rational
The square root of b is never rational

Answer 2

A) True B)False C) True D) True E) False F) True

Explanation:

We are given the following information in the question:

A is a rational number and B is an irrational number.

A) True

The sum of A and B will always be irrational.

B)False

We will show this with the help of a counter example.

2 is a rational number and √2 is an irrational number but their product is irrational.

`2* \sqrt2 = 2\sqrt2`

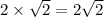
C) True

For example:
`\sqrt2* \sqrt2 = 2\text{ which is rational}, \sqrt2* \sqrt3 = \sqrt6\text{ which is irrational}.`

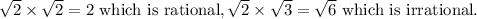
D) True

Square of a rational number will always be a rational number.

E) False.

We will prove thus with the help of a counter example.

`√(16) = \pm 4\text{ which is a rational number}`

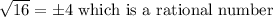
F) True

Square root of a irrational number will always be irrational.