1. We have the formula for the volume of sphere:
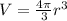
where
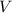
is the volume

is the radius
We know from our problem that the volume of our spherical balloon is
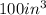
, so
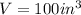
. Lets replace that value in our formula and solve for

:
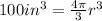

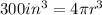

![r= \sqrt[3]{(300in^3)/(4 \pi ) }](https://img.qammunity.org/2019/formulas/mathematics/middle-school/22gaxfw1vrttjev8uwtqg28t0ikqeql5yl.png)
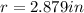
We can conclude that the radius of our spherical balloon is approximately 3 inches long. Therefore, the correct answer is
A. 3 in.
2. Lets simplify each one of the expressions first:
F. 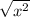
since the radicand is elevated to the same number as the index of the radical, we can cancel the radical and the exponent:
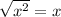
Since
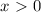
, this expression is equal to

.
G. ![(1)/(2) \sqrt[3]{8x^3}](https://img.qammunity.org/2019/formulas/mathematics/middle-school/48e47cnu9vthf1diim2cwanupfu1cw3soj.png)
8 can be expressed as
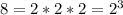
, so we can rewrite our radicand:
![(1)/(2) \sqrt[3]{8x^3} =(1)/(2) \sqrt[3]{2^3x^3} = (1)/(2) \sqrt[3]{(2x)^3}](https://img.qammunity.org/2019/formulas/mathematics/middle-school/c6a1ag5ngextzkteoqchk76ixvh6b14lep.png)
Since the radicand is elevated to the same number as the index of the radical, we can cancel the radical and the exponent:
![(1)/(2) \sqrt[3]{(2x)^3}= (1)/(2) (2x)](https://img.qammunity.org/2019/formulas/mathematics/middle-school/4bo9afa4nqtpx0de1nhb4d6zhbs1t2c8qs.png)
Now, we can cancel the 2 in the denominator with the one in the numerator:

Since
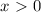
, this expression is equal to

.
H. ![\sqrt[3]{-x^3}](https://img.qammunity.org/2019/formulas/mathematics/middle-school/wb64wk5u2rbase6wo3hoxpl1o1qs5j8c56.png)
The radicand is elevated to the same number as the index of the radical, so we can cancel the radical and the exponent:
![\sqrt[3]{-x^3}=-x](https://img.qammunity.org/2019/formulas/mathematics/middle-school/mr63vjnecu9inhdoorb6xlc3fms4n5l5a2.png)
Since
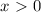
, this expression is NOT equal to

.
We can conclude that the correct answer is
H. ![\sqrt[3]{-x^3}](https://img.qammunity.org/2019/formulas/mathematics/middle-school/wb64wk5u2rbase6wo3hoxpl1o1qs5j8c56.png)
.
3. The fourth root of
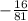
is
![\sqrt[4]{ -(16)/(81) }](https://img.qammunity.org/2019/formulas/mathematics/middle-school/3xt3t1yd277snpluvwyasdxteueyis78ka.png)
. Remember that negative numbers don't have real even roots since a number raised to an even exponent is either positive or 0. Since 4 is even and
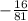
is negative, we can conclude that
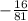
has not a real fourth root.
The correct answer is
D. no real root found.
4. This time we are going to take a different approach. We are going to simplify
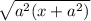
first, and then, we are going to compare the result with our given options:
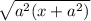
Lets apply the product rule for a radical
![\sqrt[n]{ab} = \sqrt[n]{a} \sqrt[n]{b}](https://img.qammunity.org/2019/formulas/mathematics/middle-school/vwyjul2kteeon70zztsskp9n764jzi6key.png)
:
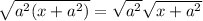
Notice that in our first product the radicand is raised to the same number as the index, so we can cancel the radical and the exponent:
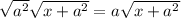
We can conclude that the correct answer is
F. 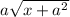 5.
5. Just like before, we are going to simplify
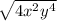
firts, and then, we are going to compare the result with our given options. To simplify our radical expression we are going to use some laws of radicals:
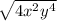
Applying product rule for a radical
![\sqrt[n]{ab} = \sqrt[n]{a} \sqrt[n]{b}](https://img.qammunity.org/2019/formulas/mathematics/middle-school/vwyjul2kteeon70zztsskp9n764jzi6key.png)
:
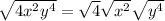
Notice that
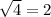
, so:
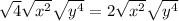
Notice that
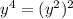
, so we can rewrite our expression:
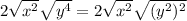
Applying the radical rule
![\sqrt[n]{a^n} =a](https://img.qammunity.org/2019/formulas/mathematics/high-school/xlyf91tckn0pymw5q1gv57jnrv24iet4bt.png)
:
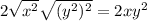
We can conclude that the correct answer is
A. 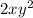
.
5. Lets check our statements:
F. 
is always greater than
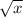
.
If

,
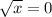
. Therefore, this statement is
FALSE.
G. 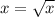
only if

. For a number bigger than zero the square root of that number will be always less than the number; therefore, this statement is
TRUE.
H. Using a calculator we can check that
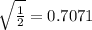
and
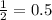
. Since
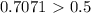
, we can conclude that
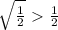
.
We can conclude that this statement is
TRUE.
J. 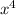
is always bigger than

.
If

and
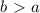
,
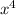
will always be smaller than

. Therefore, we can conclude that this statement is
FALSE.
6. We know that the formula for the volume of cube is
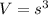
where
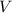
is the volume

is the side
We know for our problem that a cubical storage bin has a volume of 5832 cubic inches, so
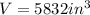
. Lets replace that value in our formula and solve for

:
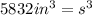
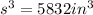
![s= \sqrt[3]{5832in^3}](https://img.qammunity.org/2019/formulas/mathematics/middle-school/mk6lh6p78i3qub6hsge737r6zix10gleol.png)
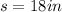 We can conclude that the length of the side of the cubical storage bin is 18 inches.
We can conclude that the length of the side of the cubical storage bin is 18 inches.