From the given picture, we see that two sides and one angle is given
Using them we have to find the value of angle C
side AB=c=14 in
side BC=a=18 in
angle A= 110 degree
Now plug these values into sine formula
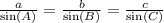
or
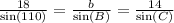
or
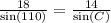
or
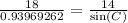
or
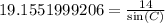
or
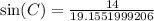
or
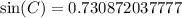
or
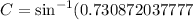
C=46.959549954213535880191108778655
Which is approx 47 degree.
Hence final answer is C=47 degree.