Question

Determine the value of r such that the line through (5, r) and (2, 3) is perpendicular to the line y = 2x ­- 4

r = 1.5

r = 9

r = ­- 3

r = 4.5

Answer 1

so, what's the slope of y = 2x - 4? well, is in slope-intercept form, thus


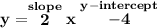
`\bf y=\stackrel{slope}{2}x\stackrel{y-intercept}{-4}` , so is 2.

now, a perpendicular line to that, will have a negative reciprocal slope to it, thus


`\bf \textit{perpendicular, negative-reciprocal slope for}\quad 2\implies \cfrac{2}{1}\\\\ negative\implies -\cfrac{2}{ 1}\qquad reciprocal\implies - \cfrac{ 1}{2}`

so, that's its slope of that perpendicular line.

but we also know that it runs through (5,r) and (2,3), so that slope is equal to -1/2