Question

The point-slope form of the equation of the line that passes through (–5, –1) and (10, –7) is y + 7 = (x – 10). What is the standard form of the equation for this line?

2x – 5y = –15
2x – 5y = –17
2x + 5y = –15
2x + 5y = –17

Answer 1

2x + 5y = –15.

Explanation:

We are given coordinates of the line passed through (–5, –1) and (10, –7) .

Applying slope formula,

`Slope=(y_2-y_1)/(x_2-x_1)`

`\left(x_1,\:y_1\right)=\left(-5,\:-1\right),\:\left(x_2,\:y_2\right)=\left(10,\:-7\right)`

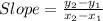
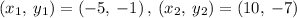
Therefore,

`m=(-7-\left(-1\right))/(10-\left(-5\right))`

`m=-(2)/(5)`

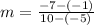
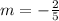
Therefore, slope is
`m=-(2)/(5)`.

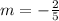Applying point-slope form
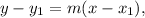`y-y_1=m(x-x_1),` we get

`y+7 = -(2)/(5)(x-10)`

`y+7=-(2)/(5)(x-10)`

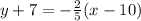
On multiplying both sides by 5, we get

`5(y+7)=5*-(2)/(5)(x+1)`

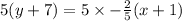
5y+35=-2(x-10)

5y+35=-2x+20

Adding 2x on both sides, we get

5y+25+2x=-2x+20+2x

2x+5y+35=20

Subtracting 35 from both sides, we get

2x+5y+35-35=20-35

2x+5y=-15.

Therefore, required equation is :

2x + 5y = –15.