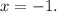Answer: The required value of x is
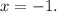
Step-by-step explanation: We are given to find the excluded value for the following rational expression:
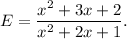
First, we need to factorize both numerator and denominator and then we should check the values of x for which the expression becomes undefined.
We have
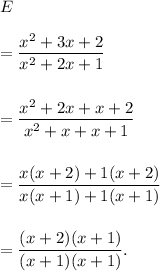
Now, we can cancel
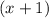 by
by
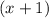 , only if
, only if
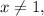 because
because
if
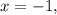 then
then
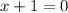 and we cannot divide 0 by 0.
and we cannot divide 0 by 0.
Therefore, if
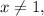 then
then
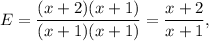
which is again well-defined because
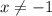 and so the denominator never become zero.
and so the denominator never become zero.
Thus, the excluded value of x is