Question

Which of these statements is true for f(x) = 5 • (6)x?

A. It is always decreasing.
B. The y-intercept is (0, 5).
C. The y-intercept is (0, 1).
D. The domain of f(x) is x > 0.

Answer 1

Option B - The y-intercept is (0, 5).

Explanation:

Given : The function
`f(x)=5\cdot 6^x`

To find : Which of these statements is true for function ?

Solution :

The exponential function is in the form
`f(x)=ab^x`

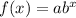
where, a is the initial amount and b is the growth/decay rate factor.

and
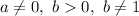`a\\eq 0,\ b>0,\ b\\eq 1` and x is any real number.

To check the statement is true or not,

A) It is always decreasing.

Function
`f(x)=5\cdot 6^x`

An exponential function is increasing when b>1,

As 6>1 it is increasing function.

So, It is false.

B) The y-intercept is (0, 5).

y-intercept means the value of x is 0.

`f(0)=5\cdot 6^0`

`f(0)=5`

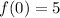
The y-intercept is (0,5).

So, It is true.

C) The y-intercept is (0, 1).

The y-intercept is (0,5) solved in part B.

So, It is false.

D) The domain of f(x) is x > 0.

Domain is defined as the possible value of x where function is defined.

The domain of exponential functions is all real numbers.

So, It is false.

Therefore, Option B is correct.

Answer 2

Given equation is
`f(x)=5 (6)^x`

Now we need to choose correct statement(s) from the given choices.

(A): It is always decreasing.

Given function is an exponential function with growth factor (6) which is more than 1. Hence it will be increasing function.

So this choice is FALSE.

(B): The y-intercept is (0, 5).

y-intercept can be found by plugging x=0 into given equation

`f(x)=5(6)^0=5(1)=5`

which same as given y-intercept (0,5)

So this choice is TRUE.

(C): The y-intercept is (0, 1).

As shown above, y-intercept is (0,5) not (0,1)

So this choice is FALSE.

(D): The domain of f(x) is x > 0

For any exponential function, domain is all real number not just x>0,

So this choice is FALSE.