Question

A box without a top is made from a rectangular piece of cardboard, with dimensions 4 m by 2 m, by cutting out square corners with side length x.

Which expression can be used to determine the greatest possible volume of the cardboard box?
(x−4)(x−2)x

(x−4)(x−2)x

(4−2x)(2−2x)x

(4x−2)(2x−4)

Answer 1

The expression that can be used to find the volume of the cardboard box is:

(4−2x)(2−2x)x

Explanation:

A box without a top is made from a rectangular piece of cardboard, with dimensions 4 m by 2 m, by cutting out square corners with side length x.

i.e. the box is in the shape of a cuboid.

Now the volume of a box is same as the volume of a cuboid.

We know that the volume of a cuboid is given as:

Volume of cuboid=Length×Breadth×Height.

So, the length of the cuboid box is: 4-2x

and the width of the box is: 2-2x

Also, the height of box is: x

Hence, the volume of cuboid is:

`Volume=(4-2x)* (2-2x)* x\\\\Volume=(4-2x)(2-2x)x`

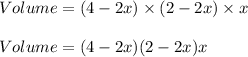
Hence, the expression for the volume of cuboid box is:

(4−2x)(2−2x)x