Question

The graphs of y=x^2-3 and y=3x-4 intersect at approximately...

Answer 1

Point at which they intersect is going to have a single y value and a single x value. So at that point, the x and y values are equal:


`y=x^(2)-3 \\ y=3x-4 \\ x^(2)-3=3x-4 \\ x^(2)-3x+1=0 \\ x= \frac{-b± \sqrt{b^(2)-4ac} }{2a} \\ x= (3± √(9-4) )/(2) \\ x= (3± √(5) )/(2) \\ x=2.62, 0.38`

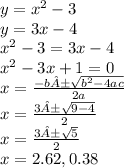
So the lines intersect at two x values, 2.62 and 0.38. Now plug them into either equation to find the y values:


`y=3(2.62)-4 \\ y=3.86`


`y=3(0.38)-4 \\ y=-2.86`

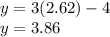
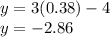
So the lines intersect at (2.62,3.86) and (0.38,-2.86)