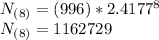Question

If the initial population size is 996 plants and the geometric rate of increase is 2.4177, calculate the population size after eight years for the annual plant phlox drummondii.

Answer 1

Population after eight years is equal to
`1162729`

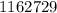
Step-by-step explanation:

Given -

Initial population size of the plant is equal to
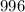`996` plants

The population of plants is increasing geometrically.

The rate of geometric growth of population is equal to
`2.4177`

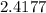
The population size is to be determined after eight years.

Geometric growth is determined by

`N_((t)) = N_0* \alpha ^t`

Where

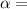`\alpha =` rate of increase of population growth

Substituting the given values in above equation, we get

`N_((8)) = (996)*2.4177^8\\N_((8)) = 1162729`

Answer 2

Initial population size = 996
Geometric rate of increase = 2.4177
Duration = 8 years

Final population size = 996 * 2.4177^8
= 996 * 1167.3989
= 1,162,729.3

Therefore, the population size after eight years for the annual plant phlox drummondii is approximately 1,162,729