Question

∠1∠1 and ​ ∠2∠2 ​ are a linear pair, and ​ ∠2∠2 ​ and ​ ∠3∠3 ​ are vertical angles. m∠2=(5+4y)∘m∠2=(5+4y)∘ and ​ m∠3=(6y−25)∘m∠3=(6y−25)∘ . What is m∠1m∠1 ?

Answer 1

`{\angle}1=115^(\circ)`

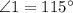
Explanation:

It is given that the ∠1 and ∠2 forms a linear pair and ∠2 and ∠3 are the vertical angles.

Also, we are given that the measure of the ∠2 is ∠2=(5+4y)° and the measure of ∠3 is ∠3=(6y-25)°.

Since, ∠2 and ∠3 forms vertical angles, thus they will be equal in measure, hence

`{\angle}2={\angle}3`

⇒
`(5+4y)^(\circ)=(6y-25)^(\circ)`

⇒
`5+25=6y-4y`

⇒
`30=2y`

⇒
`y=15^(\circ)`

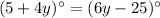
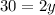
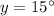
Therefore, the measure of ∠2 will be:

`{\angle}2=5+4(15)=5+60=65^(\circ)`

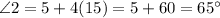
Now, ∠1 and ∠2 forms linear pair, therefore

`{\angle}1+{\angle}2=180^(\circ)`

⇒
`{\angle}1+65^(\circ)=180^(\circ)`

⇒
`{\angle}1=115^(\circ)`

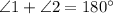
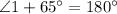
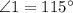
Hence, the measure of ∠1 is
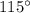`115^(\circ)`.

Answer 2

Linear pair of angles ads up to 180°. Vertical angles have same value.
According to this we have:
m<1 + m<2 = 180°
m<2=m<3

We can use this to solve for m<1.
m<2=m<3
5+4y=6y-25
4y-6y=-25-5
-2y=-30
y=15
m<2=5+4*15
m<2=65°

m<1 + m<2 = 180°
m<1 + 65° = 180°
m<1 = 180° - 65°
m<1 = 115°