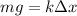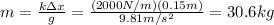Question

A spring with a spring constant of 200N/m is compressed 15cm when a mass is placed on top of it. What is this mass?

Answer 1

The weigth of the mass placed on top of the spring provides the force that compresses it:

`F=mg`
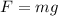
where m is the mass and g is the gravitational acceleration.

For Hook's law, the compression
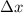
`\Delta x` of the spring is related to the force applied by

`F=k \Delta x`
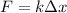
where k is the spring constant. Using
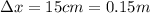
`\Delta x= 15 cm= 0.15 m` and k=200 N/m, we can equalize the two forces to find the mass m:

`mg=k \Delta x`

`m= (k \Delta x)/(g)= ((2000 N/m)(0.15 m))/(9.81 m/s^2)=30.6 kg`