Answer:
The average rate of change is 3.
Explanation:
The given points are
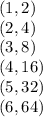
Notice that the relation between coordinates is exponential, because y-values are the result of a power with base 2, and x-values represents exponents.
The function that defines this sequence is
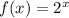
Where the factor that creates this geometric sequence is 2.
However, when we talk about the average rate of change, it's defined as
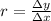
In words, it's the quotient between the change of vertical values and the change of horizontal values.
In this case, we have
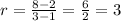
Therefore, the average rate of change from n = 1 to n = 3 is 3.