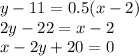Question

The endpoints of a side of rectangle ABCD in the coordinate plane are at A (2, 11) and B (7, 1). Find the equation of the line that contains the given segment. The line segment is AD. The equation is y = .

Answer 1

Explanation:

Given that ABCD is a rectangle. A is (2,11) and B (7,1)

To find equation of AD

AD is perpendicular to AB and passes through A

To find slope of AB

Slope = change in y/change in x =
`(1-11)/(7-2) =-2`

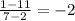
Slope of AB = slope of perpendicular line =
`(-1)/(-2) =0.5`

Using point slope formula we get equation of AD is

`y-11=0.5(x-2)\\2y-22 =x-2\\x-2y+20 =0`

Answer 2

we know that
A (2, 11) and B (7, 1)

step 1
find the slope of a line AB
the slope m=(y2-y1)/(x2-x1)------> m=(1-11)/(7-2)---> m=-10/5----> m=-2

step 2
find the equation of a line AD

we know that
the segment AB and the segment AD are perpendicular
so
m1*m2=-1
m2=-1/m1-----> m2=1/2

with the slope m2=1/2 and the point A(2,11)
y-y1=m*(x-x1)------> y-11=(1/2)*(x-2)----> y=(1/2)x-1+11
y=(1/2)x+10----> y=0.5x+10

the answer is
the equation of a line AD is y=0.5x+10

see the attached figure