Completing the square is a method of factoring as well as a way to put quadratic equations into vertex form to find the vertex and then the focus and directrix. We are using it here to factor and find the zeros of that parabola. Begin by moving the constant to the other side of the equals sign.
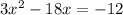
. In order to complete the square, the leading coefficient on the x-squared term HAS to be a 1. Ours is a 3. So we will factor it out:
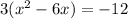
. Take half the linear term, square it, and add it to both sides. Our linear term is 6. Half of 6 is 3 and 3 squared is 9. So we add in 9...but don't forget about that 3 we factored out. It refuses to be forgotten. It is a multiplier, so what we have actually added in was 3*9= 27. Like this:
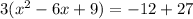
. Now we will do the math on the left and on the right we will express what's in parenthesis as the perfect square binomial we created in the process of completing the square.
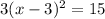
. Divide both sides by 3 to get

. Undo that square on the left by taking the square root of both sides.
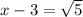
and
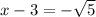
. Solving for x we get the 2 solutions of
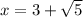
and

. Those solutions in decimal form are x = 5.24 and x = .76