Question

1. Suppose you invest $5010 at an annual interest rate of 6.4% compounded continuously. A.) Write an equation to model this. B) How much money will you have in the account after 2 years?

2. Suppose you invest $100 at 6% annual interest. Calculate the amount of money you would have after 1 year if the interest is compounded:
A.) quarterly.
B.) monthly.
C.) daily.

3. Suppose you deposit $100,000 in an account today that pays 6% interest compounded annually. Write an equation to determine how long it will take before the amount in your account is $500,000 (Note: you only have to write the equation).

I need help because I'm stuck.

Answer 1

To solve our problems, we are going to use the formula for compounded interest:
`A=P(1+ (r)/(n) )^(nt)`
where

`A` is the final amount after
`t` years

`P` is the initial amount

`r` is the interest rate in decimal form

`n` is the number of times the interest is compounded per year

`t` is the time in years

1. A) We know for our problem that the initial investment is $5010, so
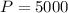
`P=5000`. We also know that the interest rate is 6.4%. To express the interest in decimal form, we are going to divide it by 100%:
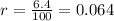
`r= (6.4)/(100) =0.064`. Since the interest is compounded continuously, it is compounded 365 times per year; therefore,
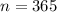
`n=365`. Lets replace those values in our formula:

`A=P(1+ (r)/(n) )^(nt)`

`A=5010(1+ (0.064)/(365))^(365t)`

We can conclude that the equation that model this situation is
`A=5010(1+ (0.064)/(365))^(365t)`

B. To find the amount of money you will have after 2 years, we are going to replace
`t` with 2 in the equation from point A:

`A=5010(1+ (0.064)/(365))^(365t)`

`A=5010(1+ (0.064)/(365))^((365)(2))`

`A=5694.6`

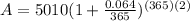
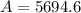
We can conclude that after 2 years you will have $5694.06 in your account.

2. We know for our problem that
`P=100`,
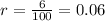
`r= (6)/(100) =0.06`, and
`t=1`.
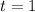
A. Since the interest is compounded quarterly, it is compounded 4 times per year; therefore,
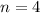
`n=4`. Lets replace the values in our formula:

`A=P(1+ (r)/(n) )^(nt)`

`A=100(1+ (0.06)/(4) )^{(4)(1)`

`A=106.14`
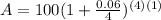
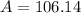
We can conclude that after a year you will have $106.14 in your account.
B. Since the interest is compounded monthly, it is compounded 12 times per year; therefore,
`n=12`. Lets replace the values in our formula:

`A=P(1+ (r)/(n) )^(nt)`

`A=100(1+ (0.06)/(12))^{(12)(1)`

`A=106.17`
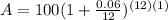
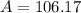
We can conclude that after a year you will have $106.17 in your account.
C. Since the interest is compounded daily, it is compounded 365 times per year; therefore,
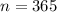
`n=365`. Lets replace the values in our formula:

`A=P(1+ (r)/(n) )^(nt)`

`A=100(1+ (0.06)/(365))^((365)(1))`

`A=106.18`
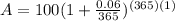
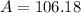
We can conclude that after a year you will have $106.18 in your account.

3. We know for our problem that the initial investment is $100,000, so
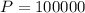
`P=100000`. We also know that the final amount will be $500,000, so
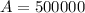
`A=500000`. The interest rate is 6%, so
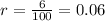
`r= (6)/(100) =0.06`. Since the interest rate is compunded anually, it is compounded 1 time per year; therefore,
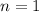
`n=1`. Lets replace the values in our formula and solve for
`t`:

`A=P(1+ (r)/(n) )^(nt)`

`500000=100000(1+ (0.06)/(1))^((1)(t))`

`500000=100000(1+0.06)^t`

`(500000)/(100000) =1.06^t`

`1.06^t=5`

`ln(1.06^t)=ln(5)`

`tln(1.06)=ln(5)`

`t= (ln(5))/(ln(1.06))`

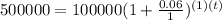
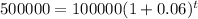
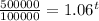
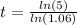
We can conclude that
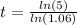
`t= (ln(5))/(ln(1.06))` is the equation to determine how long it will take before the amount in your account is $500,000

As a bonus:

`t= (ln(5))/(ln(1.06))`

`t=27.6`
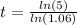
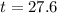
We can conclude that after 27.6 years you will have $500,000 in your account.