1) the first step to solving this is to know that any non zero expression that is raised to the power of zero will equal 1.
m³
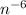
x 1
any expression multiplied by 1 remains the same
m³
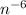
now express this with a positive exponent using
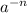
=

m³ x
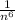
now calculate the product
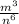
this means that the correct answer to number one is
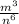
2) the first step for solving this expression is to reduce the fraction with a
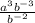
now reduce the fraction with

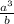
this means that the correct answer to question 2 is
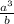
3) the first step to solving this expression is to express with a positive exponent using tex] a^{-n} [/tex] =

(

×
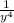
× x³ )

now calculate the product
(
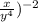
now express with a positive exponent using (
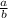
)
![[tex] x^(-n)](https://img.qammunity.org/2019/formulas/mathematics/high-school/lvvfyp5yerox16eky1phqyge20vfxpyul0.png)
= (

)

(
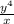
)

to raise a fraction to a power,, you need to raise the numerator and denominator to that power.

this means that the correct answer to question 3 is

let me know if you have any further questions
:)