Question

A mountain climber is at an altitude of 2.9 mi above the earth’s surface. From the climber’s viewpoint, what is the distance to the horizon? Enter your answer as a decimal in the box. Round only your final answer to the nearest tenth.

Answer 1

When climber is looking at horizon we can consider that he is looking straight at one point. We need to calculate length of a line extending from climber to horizon.
When applied to a circle this line is called tangent. Tangent is a straight line that touches circle in just one point. By definition tangent is perpendicular to a radius of circle. This will help us to solve this problem.

From the picture we can see that we have a triangle. It is right angle triangle with right angle positioned at location where tangent intercepts radius. We can use the pythagorean theorem to solve this problem:

`a^(2) + b^(2) = c^(2)`

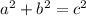
Where:
a = 3959
b = x
c = 3959+2.9=3961.9

`3959^(2) + x^(2) = 3961.9^(2) \\ \\ x^(2) =3961.9^(2) - 3959^(2) \\ \\ x^(2) =22970.61 \\ \\ x=151.6`

From the climber's viewpoint the horizon is at distance of 151.6 miles.