Question

A mountain climber is at an altitude of 2.9 mi above the earth’s surface. From the climber’s viewpoint, what is the distance to the horizon? Enter your answer as a decimal in the box. Round only your final answer to the nearest tenth.

Answer 1

151.6

because

3959^2 + x^2 = (3959 + 2.9)^2 = 151.560582

round to nearest tenth = 151.6

Answer 2

The distance to the horizon, from the climber’s viewpoint to the nearest tenth is, 151.6 mi

Explanation:

Using Pythagoras theorem:

`\text{Hypotenuse side}^2 = \text{Adjacent side}^2 + \text{Opposite side}^2`

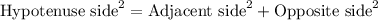
We know that:

Radius of the earth ≈ 3959 mi.

The radius of a circle meets a tangent at 90 degree.

As per the statement:

A mountain climber is at an altitude of 2.9 mi above the earth’s surface.

See the diagram as shown below in the attachment:

In triangle ABO

Hypotenuse side = AO = 3959 +2.9 = 3961.9 mi

Opposite side = AB = x mi and

Adjacent side = 3959 mi

Substitute these we have;

`3961.9^2 = 3959^2+x^2`

⇒
`15696651.6 = 15673681 +x^2`

⇒
`22970.5 = x^2`

⇒
`√(22970.5) = x`

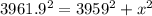
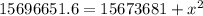
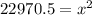
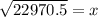
Simplify:

151.560219 mi = x

or

x =151.60219 mi

therefore, the distance to the horizon, from the climber’s viewpoint to the nearest tenth is, 151.6 mi