Answer: The required x-intercepts are (4, 0) and (-7, 0).
Step-by-step explanation: We are given to find the x-intercepts for the parabola defined by the following equation :

We know that
the x-intercepts of a function are the points where the y co-ordinate is zero.
So, from equation (i), we have
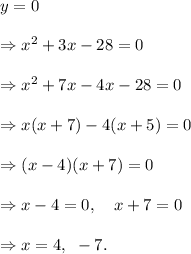
Therefore, the x-intercepts of the given function are (4, 0) and (-7, 0).