Answer:
C. 269 years
Step-by-step explanation:
First, we have to find the value of the rate constant (k) through the following expression.
![[Ar]_(t)=[Ar]_(0).e^(-k.t)](https://img.qammunity.org/2019/formulas/chemistry/middle-school/za8zn26lmh4y0w87us002kyyngk8yb27a6.png)
where,
![[Ar]_(t)](https://img.qammunity.org/2019/formulas/chemistry/middle-school/aubwu6dd6wnnzdz3jo5tu1ytzlj94syu9t.png) is the amount of Ar at a certain time t
is the amount of Ar at a certain time t
![[Ar]_(0)](https://img.qammunity.org/2019/formulas/chemistry/middle-school/v7a233tdfyk3wkiac3g4datg1kl3t0jisx.png) is the initial amount of Ar
is the initial amount of Ar
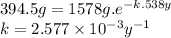
Provided the rate constant, we can find the half-life (t1/2).
t1/2 = ln 2/k = ln 2/2.577 × 10⁻³ y⁻¹ = 269.0 y