Question

A sample of argon-39 had an original mass of 1578 grams. After 538 years, the sample is 394.5 grams. What is the half-life of argon-39? A. 135 years B. 180 years C. 269 years D. 538 years

Answer 1

well uhhhh kanye loves kanye

Answer 2

C. 269 years

Step-by-step explanation:

First, we have to find the value of the rate constant (k) through the following expression.

`[Ar]_(t)=[Ar]_(0).e^(-k.t)`

where,

`[Ar]_(t)` is the amount of Ar at a certain time t

`[Ar]_(0)` is the initial amount of Ar

`394.5g=1578g.e^(-k.538y) \\k = 2.577 * 10^(-3) y^(-1)`

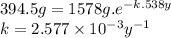
Provided the rate constant, we can find the half-life (t1/2).

t1/2 = ln 2/k = ln 2/2.577 × 10⁻³ y⁻¹ = 269.0 y