This is a compound interest problem, therefore s(t) should be in the form:
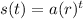
where:
t = time in years
s(t) = the value of your item after t years
a = the initial value of your item
r = rate
Therefore, we already know that a = 245$.
Now, we can calculate r:
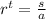
![r = \sqrt[t]{ (s)/(a) }](https://img.qammunity.org/2019/formulas/mathematics/college/bcqeiroxjsaequ9y2bjntfurc35tcl85mx.png)
![r = \sqrt[5]{ (560.50)/(245) }](https://img.qammunity.org/2019/formulas/mathematics/college/a56gsp16jmd2qf0nvf18wy8akny5vpjvl6.png)
= 1.18
Therefore, the correct answers are
a = 245 and
r = 1.18