Question

If a moving car speeds up until it is going twice as fast, how much kinetic energy doe s it have compared with its initial kinetic enegy

Answer 1

The kinetic energy of an object of mass m and velocity v is given by

`K= (1)/(2) mv^2`

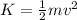
Let's call
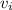
`v_i` the initial speed of the car, so that its initial kinetic energy is

`K_i = (1)/(2) mv_i^2`
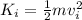
where m is the mass of the car.

The problem says that the car speeds up until its velocity is twice the original one, so

`v_f = 2 v_i`
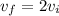
and by using the new velocity we can calculate the final kinetic energy of the car

`K_f = (1)/(2) mv_f^2 = (1)/(2)m (2 v_i)^2 = 4 ( (1)/(2) mv_i^2)=4 K_i`
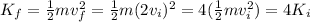
so, if the velocity of the car is doubled, the new kinetic energy is 4 times the initial kinetic energy.