Given that the diameter of a human hair
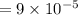
Given that the diameter of a spider's silk
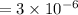
Now we have to find how much greater is the diameter of a human hair than the diameter of a spider's silk.
To find that we just need to subtract the given numbers.
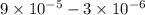
Since powers are not same so let's make them equal
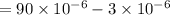
now we can easily subtract the coefficients that is 3 from 9
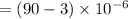
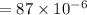
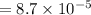
Hence final answer is
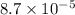 .
.