Question

Solve the linear equations by using substitution -2X-5Y=3 3X+8Y=-6

Answer 1

`\sf -2x-5y=3`

`\sf 3x+8y=-6`

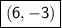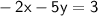
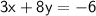
Let's solve the second equation for 'x':


`\sf 3x+8y=-6`

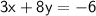
Subtract 8y to both sides:


`\sf 3x=-8y-6`

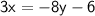
Divide 3 to both sides:


`\sf x=-(8)/(3)y-2`

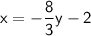
Now let's plug this in for 'x' in the first equation:


`\sf -2x-5y=3`


`\sf -2(-(8)/(3)y-2)-5y=3`

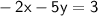
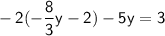
Distribute:


`\sf (16)/(3)y+4-5y=3`

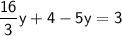
Combine like terms:


`\sf (1)/(3)y+4=3`

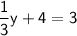
Subtract 4 to both sides:


`\sf (1)/(3)y=-1`

Divide 1/3 to both sides or multiply by its reciprocal, 3:


`\sf y=-3`

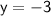
This is the y-value of our solution, we can plug it into any of the two equations to find the x-value:


`\sf 3x+8y=-6`


`\sf 3x+8(-3)=-6`

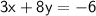
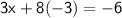
Multiply:


`\sf 3x-24=-6`

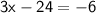
Add 24 to both sides:


`\sf 3x=18`

Divide 3 to both sides:


`\sf x=6`

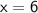
So our final solution is:


`\boxed{\sf (6,-3)}`