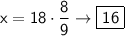Question

Can someone plz help me thank you

Answer 1

7.

Direct variation is:


`\sf y=kx`

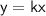
Where 'k' is the constant of variation. Let's plug in y = -6 and x = 10 into the formula:


`\sf -6=k(10)`

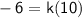
Divide 10 to both sides:


`\sf k=-(3)/(5)`

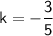
Plug this in for 'k' in our formula:


`\sf y=-(3)/(5)x`

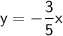
This is our formula. To find out what 'y' is when 'x' = 5, plug in 5 for 'x':


`\sf y=-(3)/(5)(5)`

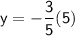
Multiply:


`\boxed{\sf y=-3}`

9.

Let's plug in y = 9 and x = 8 into our formula:


`\sf 9=k(8)`

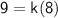
Divide 8 to both sides:


`\sf k=(9)/(8)`

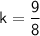
So our equation is:


`\sf y=(9)/(8)x`

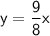
Now let's plug in 18 for 'y' to find out what 'x' is when y = 18:


`\sf 18=(9)/(8)x`

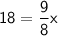
Divide 9/8 to both sides or multiply by its reciprocal 8/9:


`\sf x=18\cdot(8)/(9)\rightarrow \boxed{\sf 16}`