Answer:
The average rate of change of function is -4 in [1,3]
Explanation:
The average rate of change for graphic quadratic function for the interval from x=1 to x=3
The average rate of change of a function is change y over change in x.
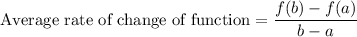
where,
a=1 and b=3
Using graph we will find f(1) and f(3)
f(3)=-8
f(1)=0
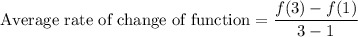
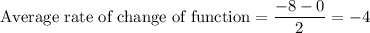
Hence, The average rate of change of function is -4 in [1,3]